BOJ) 2300 기지국
BOJ Gold 3 - DP
1. Problem
BOJ_2300 is the problem of dynamic programming. The level of problem is Gold 3.(Link of the problem of BOJ)
Inputs
- The number of buildings: N (1≤N≤10,000)
- The position of ith building for each row: x, y (|x|, |y| ≤ 1,000,000)
Conditions
- The y-coordinate of all buildings are not 0.
- The line of communication equals x-axis.
- Base stations must on the line of communication. It means the y-coordinate of all base stations are 0.
- The range of communication by a base station is the square centered on the base station.
- All buildings have to be in the ranges of communication.
- The cost of constructing all base stations is sum sides of all ranges of communication
Outputs
- The minimal cost of cost of constructing all base stations.

In the figure above, the answer is 9. There are 7 buildings, (-4, -1), (-2, -1), (0, 2), (1, -1), (3, 1), (5, 1), (8, -1). And, by the answer, there are 3 base stations, (-2, 0), (2, 0), (6.5, 0).
2. Approach to the problem
This problem is an usual problem of dynamic programming with partition. It is similar with the well-known problem called Matrix-Chain Multiplication problem. The main problem is finding ranges of communications with minimal sum of construction cost. It can be divied some subproblems, if the problem is divided the group of buildings whose x-coordinate is consecutive. In the fig 1, the main problem consists of 7 buildings. We can find directly 3 subproblems-each of them have one range of communication. It is correct, because the perperty of base station and rnages of communication. $y$-coordinate of base station is always 0, and a ranges of communication is square. The vertices in a range are covered by a square of edge is 2maximal $y$-coordinate. So, non-end vertices must be covered. Otherwise, if a square of edge is 2maximal $y$-coordinate can not cover all vertics, then a square of edge is distance about $x$-coordinate of two end vertics. In this case, because this square has more longer edge than the maximal $y$-coordinate, all vertics are covered. And intuitively main problem and subproblems have same structures. Because subproblems defined with buildings whose x-coordinate is consecutive are independent of each other and the solution is the minimal value, moreover, the optimal solution is sum of optimal subsoltion. That is, there is an optimal substructure.
Dividing the main problem into 3 subproblems makes solution complicated. So, let’s divide the main problem into 2 subproblem. Because we have to consider all possible case, we solve all case and compare them. So, the soltion can be expressed as recursion, if the solution about buildings from ith to jth after sorting by x-coordinate is defined as T(i, j).
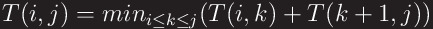
There are overlapping problems. For example, by the definition above, we have to solve T(1, 3) and T(1, 4) to solve T(1, 6). T(1, 3) and T(1, 4) include T(1, 2).
3. Solve the problem: How to apply DP
Before solve the problem using the definition above, we have to tranform the recursion. The recursion does not include grouping N buildings in one range of communication. Futhermore, although the problem size of T(1, 3) and T(4, 6) are same, the buildings of each problem are not same. So, we have to solve a lot of problems. Think about the definition. The each case of T(1, N) includes T(1, 1), T(1, 2), ... , T(1, N-1). They have overlapping problems with same buildings. And, we just try grouping the rest of buildings into one range of communication, bucause the solution is the minimal value. If the group makes more cost, just drop the case and choose the other case. It is correct because the groups of buildings are perfectly independent. For exmaple, the optimal solution of T(1, 4) consists of groups (1..2), (3..4). Then, we already solve T(1, 1), T(1, 2), T(1, 3). Think about T(1, 5). If the optimal solution of T(1, 5) includes (5), the optimal solution consist of groups (1..2), (3..4), (5). It means T(1, 5) is solved by T(1, 4) and one range including the 5th building. Otherwise, if the optimal solution of T(1, 5) includes (4..5), we can’t use the optimal solution of T(1, 4). Because the solution of T(1,4) includes the group (3..4) that conflicts with the group (4..5). But we can use T(1, 3) that is already solved. So, T(1, 5) is solve by T(1, 3) and one range including the 4th building and the 5th building. So, we can change the definition as below.
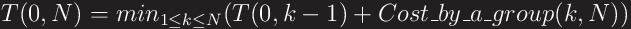
We start k from 0 to include a group including whole buildings. T(0,0) is the base case. The optimal solution of the base case is 0.
Solving Cost_by_a_group(k,N) is easy. The maximal height (absolute value of the y-coordinate of buildings) in the problem makes the biggest range of communication, and this range must exist. So, if the biggest range can include all buildings in the range, we don’t need to consider other ranges. Else, the optimal range of communication must include the leftmost building at its left side and the rightmost building at its right side. Because we consider the biggest range made by the building whose height is maximal height among the buildings in the problem first, it is guarnteed the optimal range is bigger than the biggest range made by the building.

Finally, the definition of problem is fixed.

By the definition, constructing the algorithm is easy, using double nested iteration. The outer iteration with iterator i defines the size of a problem, T(1, i). The inner iteration with iterator j is the size of buildings grouped by one range of communication, Cost_by_a_group(j,N). The iterator j decrease by one from i, updating the maximal height among the buildings.
4. Time Complexity
There are a double nested iteration. And, Cost_by_a_group(j,N) is solve in O(1) time using an array to store buildings. So, total time complexity is O(N2).
5. Source Code
You can watch the source code clearly in this github link.
Refers
Sang-Hwa-Lee, “[BOJ/백준][Gold3] 2300 : 기지국 (C++)”