Sorting ②) Merge Sort (feat. BOJ 2751)
BOJ Silver 5
1. Problem
BOJ_2751 is the problem of sorting numbers using array. Given integers, sort it in an increasing order. Input is the number of the integers named N (1 <= N <= 1,000,000) and the integers which never overalp. Output is the integers, which were inputted, in increasing order for each line. The time limit of the problem is 2 seconds, and the memory limit is 256MB. The level of problem is Silver5.(Link of the problem of BOJ)
2. Approach to the problem
The time limit of this problem is 2 seconds, bigger than BOJ_2750. But the number of integers given are 1,000 times bigger. So, if using Bubble Sort, Insertion Sort, Selection Sort or etc, we can’t solve this problem. The time complexity of algorithm I’ve mentioned is O(n2). Because the input size is 1,000,000, it needs 10,000 seconds, assuming we need 1 second to execute 100,000,000 primitive operators. So, we have to use the sorting algorithm whose time complexity is ensured less than O(n2). Such as Merge Sort, Heap sort whose time complexity is ensured O(nlogn).
For solving this problem, I will be applying Merge Sort.
3. Merge Sort
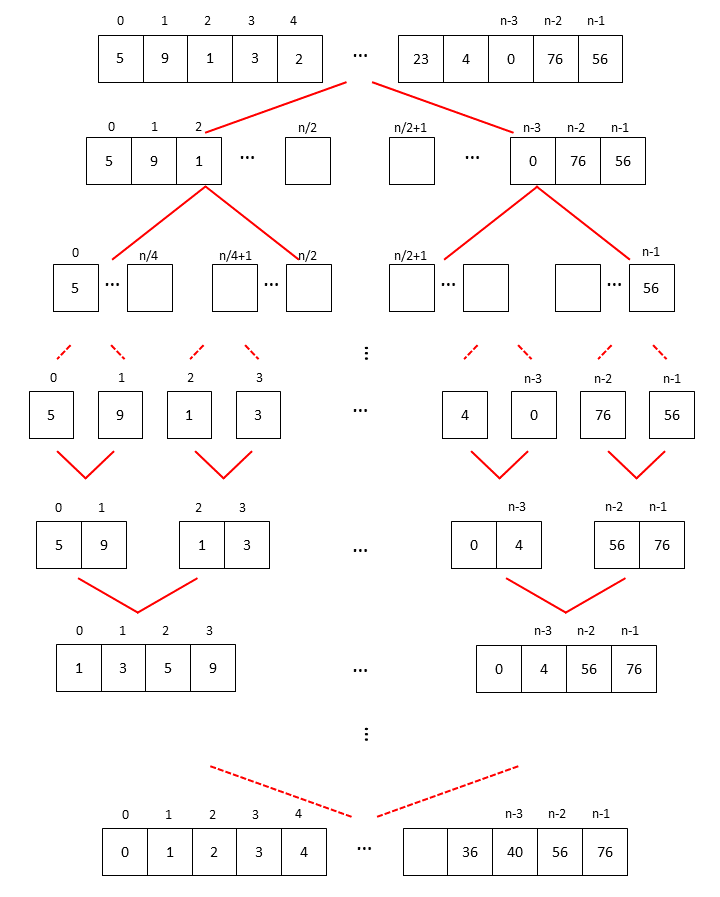
Merge Sort is the basic sorting algorithm applied divide-and-conquer. Similar to Binary Search, in Merge sort you divide the sequence length into half until it reaches 1, which is the base case.
Next, you sort and merge the subsequences from the base case, all the way to the original problem. When merging the subsequences, there are two subsequences. Make a new sequence(buffer) for the result of merging. Compare the minimum numbers of the subsequences, insert the less minimum number to the result sequence, and remove the number from the original subsequence. Iterate this process until subsequences are empty. In base case, the length of subsequence is just 1. Therefore, the subsequence of base case is sorted. This means we can easily compare what number is smallest. When comparing them, we just compare the first element of each subsequence.
4. Time Complexity & Space Complexity of Merge Sort
We divide the original sequence until the sizes of subsequences are 1. So, we need to spend O(n) time to divide them. Although the length of original sequence is an odd number, it doesn’t matter because floor and ceiling function is ignored in asymptotic notation. In each dividing process, we need buffers for each dividing process. And we also move half of original sequence and subsequences each process to buffer. So, we need O(n) space to store subsequences. And because the length of subsequences in level i is (n/2i), the height is log n.
When merging the subsequences, there are two subsequences and one buffer sequence for result of merging and sorting them. So, we need O(n) space. Because all subsequence is already sorted, only O(n) time is spent to merge in each level. Therefore, we have O(logn) levels. So, the time complexity of merge process is O(nlogn).
Finally, the time complexity of Merge Sort is O(n) + O(nlogn). However, O(nlogn) dominate O(n) in asymptotic notation, On the other hand, the time complexity is O(nlogn). And the space complexity is O(n).
5. Psuedocode & Source Code
MergeSort
Input A is the unsorted array of integers
Output the sorted array A
if A.size == 1 then return
subArray1 = A[0..(1/A.size)]
subArray2 = A[(1/A.size)..(A.size-1)]
MergeSort(subArray1)
MergeSort(subArray2)
Merge(A, subArray1, SubArray2);
Merge
Input A is the unsorted array of integers, subArray1 and subArray2 is the subarray of A
Output the sorted array A
for i == 0 to i = A.size-1
A[i] = the less number between the smallest number of subArray1 and the smallest number of subArray2
remove from the number selected from original subArray.
You can watch the source code clearly in this github link.