1. Problem

  BOJ_2533 is the problem of dynamic programming using general tree. The level of problem is Gold 3.(Link of the problem of BOJ)
  Input is the number of vertex(node) of tree N (2 <= N <= 1,000,000), edges(v, w), where v and w is vertex(node) of tree. There are two kinds of vertices, Early adopter(TEA), and Not Early adpopter(FEA). If all adjacent nodes of node v are TEA, then v accepts a new idea.
  Output is the minmal number of TEA nodes when all nodes are TEA or accept a new idea.

2. Approach to the problem

  This problem is usual problem of dynamic programming using general tree. We have to consider two cases per a node, TEA or not. Because computing all case needs O(2^N) time, brute force is not correct.


fig 1. Overlapping problems

  First, There are overlapping problems. Think about node v whose children is w and u. For solving the problem of the tree rooted by v, we have to solve the problem of the subtree rooted by w and u.

fig 2. Optimal substructure

  Second, There is optimal substructure. The structure of the problem of the subtrees rooted by children of v is same with the problem of the tree rooted by v. Whether a node is TEA or not is only affected by adjacent nodes. So, when computing the solution of the tree rooted by v, we just sum the optimal solution of subtrees rooted by children of v and add 1(v is TEA) or not(v is FEA).

3. Solve the problem : How to apply DP


fig 3. Cases of optimal solution

  Divide the main problem into subproblems consist of subtrees. Think about node v whose children is w and u. First, when v is FEA, two children of v must be TEA. If we already have the minimal number of TEA nodes of subtrees rooted by w and u, the minimal number of TEA nodes of the tree rooted by v is sum of the minimal numbers of TEA nodes of subtrees of children. Second, when v is TEA, whether each child of v is TEA or not is not matter. So, just sum the minimum of the minimal number of TEA nodes of two cases of each subtree rooted by children. And, add 1 because v is TEA.
  We use memoization two dimensional matrix teaNum. The elements of the matrix is the minimal numbers of TEA. Node idices are mapped to the first dimension(row). The cases of each nodes are mapped to the second dimension(column). So, we can define teaNum[node][case] as


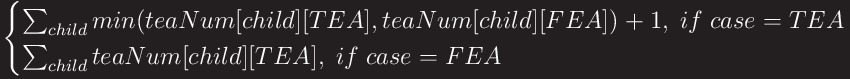
  After running the memoization, we can get the minimal number of TEA nodes of the tree of main problem.


Key points: Do not solve base case

  To define the base case is important in recursion including Divide-and-Conquer, Dynamic Programming and etc. If the base case is defined not well, the algorithm run forever or comute an incorrect output. Generally, the base case have to compute the optimal output in dynamic programming. Using the matrix above, however, the base case of our recursive algorithm compute an incorrect ouput. Think about the tree whose |nodes| is 1. The correct answer is 1, because the root have to be TEA. min(teaNum[root][TEA], teaNum[root][FEA]) is 0, however, because teaNum[root][TEA] is 1 and teaNum[root][FEA] is 0.
  But, we have to keep the same way of memoization for solving main problem. Don’t break the rule, and just handle exception about the number of nodes of a tree is 1. Fortunately, in this problem, the number of nodes is greater than 1, so we don’t need to handle that.
  We need to consider one more case, the number of children of root is 1. Because the tree is given as the set of edges, we need to construct a tree from a graph. So, when the algorithm run recursively, we need which adjacent node is the parent. The information about parent is only known using what node is visited before. In the same context, we use the information of a graph to detect base case. The base case is the node that is currently been computing is leaf. That means the number of adjacent nodes is 1(parent). If the number of children of root is 1, however, root is consider as base case, and the algorithm will be over. So, we have to add a condition to detect base case well, “the node is not root.”



4. Time complexity

  We visit all nodes once, and compute memoization table in O(1) time. So, the time complexity is O(N).

5. Source Code

You can watch the source code clearly in this github link.