1. Problem

  BOJ_2750 is the problem of sorting numbers using array. Given integers, sort it in an increasing order. Input is the number of the integers,N (1 <= N <= 1,000), and the integers which never overlap. Output is the integers, which were inputed, in increasing order for each line. The time limit of the problem is 1 second, and the memory limit is 128MB. The level of problem is Bronze2.(Link of the problem of BOJ)


2. Approach to the problem

  I tried to solve the problem using 3 basic sorting algorithms, Bubble Sort, Insertion Sort and Selection Sort, as the problem requires the solution running in O(n2) time. However, in this post, I will describe only BubbleSort.


3. Bubble Sort

How to work in BubbleSort


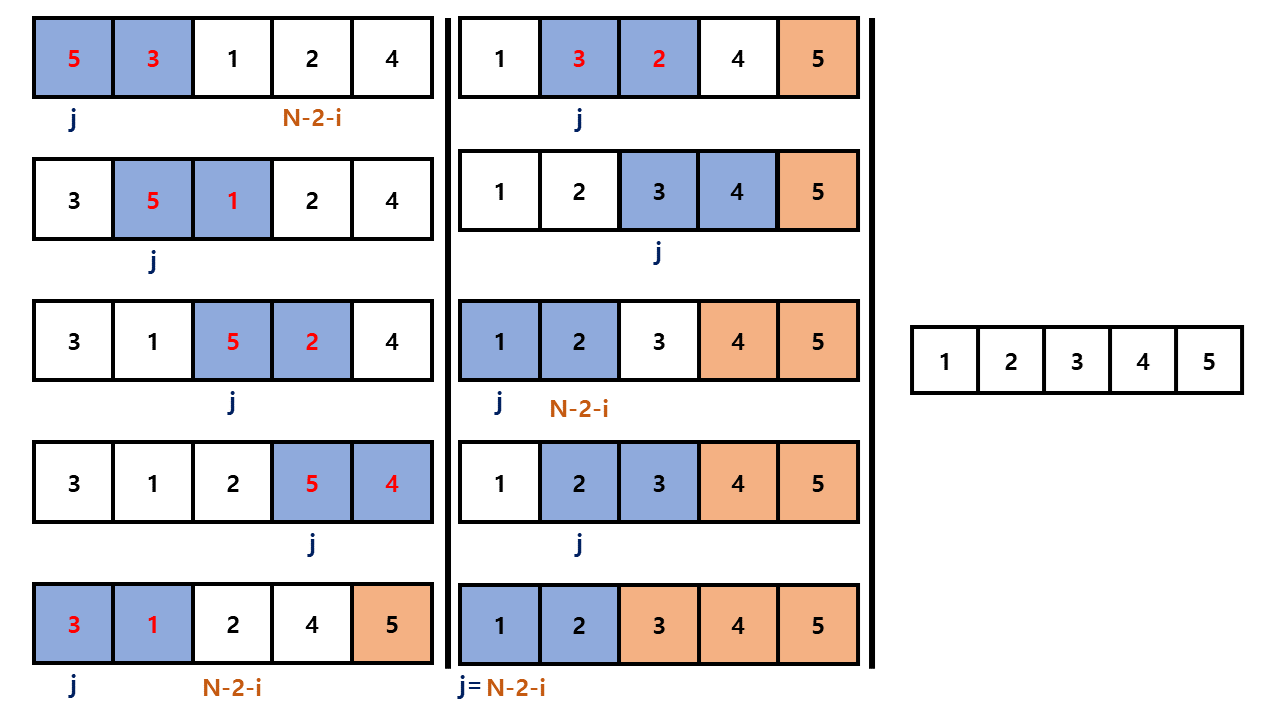
  BubbleSort is the basic sorting algorithm in which all elements are compared to the adjacent cell of themselves using double iteration. At first, the idea is dividing the problem as moving just one number-the maximum number-to the last cell. In the inner iteration, increasing the iterator j is initialized as 0(start number) to N-2. It is compared with arr[j] and arr[j+1] in each repeat. If arr[j] is larger than arr[j+1], swap them. If the iterator f increases to N-1(not N-2), it occurs Runtime error by OUT-OF-RANGE beacuse it will be compared arr[N-1] and arr[N] when the iterater f is N-1.

  In order to sort all the elements, it is necessary to repeat the inner iteration for N-1 times. Therefore, the iterator i is initialized into 0 in the outer iteration. After that, it is repeated until it increases to N-2. then the inner iteration(which moves all the maximum numbers to the last cell) will work for all elements that exist. In this situation, the algorithm run in O(n2) but It can be decreased to (n2/2) time although not affecting the growth rate.


4. Time Complexity of Bubble Sort

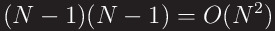
The time complexity of repeating N-1 times in each iteration


  As you can see from the formula above, the running time of the method that repeats N-1 times in each iteration is O(n2). But each time the inner iteration repeats, the numbers are sorted in decreasing order from the last cell. It means the numbers in the cells that are from the cell of which is index N-1-i to the last cell is already sorted in an increasing order. So, in each repeat, the inner iteration does not need to repeat N-1 time but just N-1-i time.

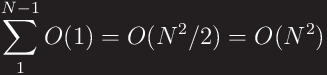
Of course, the coefficient of O(1) in the sum, in fact, is 4, but it can be ignored by asymptotic notation


  So, the time complexity is changed from O(n2) to O(n2/2)(But the coefficient of n2 is ignored in the asymptotic notation). Because Bubblesort runs in O(n2) time at any case, however, this algorithm is evaluated as ‘slow’. Even though sorting is over when in middle of the running time, BubbleSort proceeds until end of double iteration. However this can be optimized. Add the boolean variable or one integer to inspect that there is something change in the current term of first iteration. If not, break the iteration. This reduces the running times in average case. Moreover, in the best case, it makes the running time O(n) and reduce the running time in the average case.

5. Psuedocode & Source Code

BUBBLESORT WITHOUT OPTIMIZING(A)
  Input A is the unsorted array of integers
  Output the sorted array A
  for i = 0 to N-2
      for j = 0 to N-2-i
          if arr[j] > arr[j+1]
              swap(arr[j], arr[j+1])


You can watch the source code clearly in this github link.